Some ebola quarantine math
Matthew Martin
10/30/2014 10:04:00 AM
Tweetable
- Asymptomatic individuals are not infectious even if they have ebola, and
- Medically unnecessary quarantines would both harm and discourage desparately needed healthcare workers from joining the fight against ebola where it is most important: in west Africa
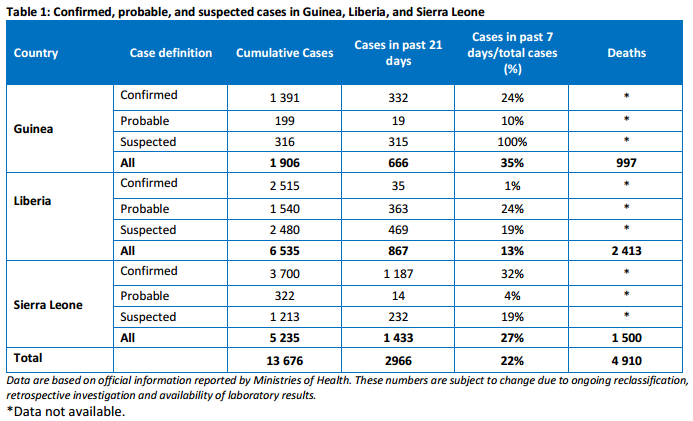
One comment I've been making in various forums is that quarantines aren't even that effective to begin with. Some 13,703 people have been infected with ebola during this epidemic, of which 521 were healthcare workers treating quarantined ebola patients. Not all infected health care workers got ebola from these patients necessarily, but the vast majority of them did. Any way you look at it, that is an astonishingly high quarantine failure rate. And don't think this is a west Africa thing: there have been two ebola transmissions within the US, and in both cases the ebola patient was quarantined at the time the transmission happened.
The ineffectiveness of quarantines further undermines the argument for mandatory quarantines of low-risk patients. To see why, here's the math. Let [$]Q[$] represent the marginal social and economic cost of quarantining an individual while [$]p[$] is the probability that an individual returning from west Africa has ebola, [$]t_u[$] is the probability that he will infect someone else given that he is not quarantined, [$]t_q[$] is the probability that he will infect others if he is quarantined, and [$]I[$] is the social and economic cost if an infection occurs. Thus, given the probability of having ebola [$]p[$] and transmission rate [$]t[$] an individual has an an expected infection cost of [$]Ipt.[$] The marginal benefit of quarantining returning health care workers from west Africa is the decrease in the expected social and economic costs from infecting others: [$]Ipt_u-Ipt_q.[$] It is beneficial to quarantine this individual if and only if the marginal benefit exceeds the costs of the quarantine itself: [$$]Ip\left(t_u-t_q\right) \geq Q.[$$] Setting this out explicitly helps clarify our thinking about the costs and benefits of a quarantine. A smaller probability of having ebola, for example, makes it less likely that a quarantine will be beneficial, as does having a lower probability of being infectious. In particular, the higher [$]t_q[$] is, the less benefits there are from quarantining and more likely it is that the quarantine will do more harm than good.
First, note that the probability that an individual arriving from west Africa has ebola--[$]p[$]--is still pretty low. The population of the three countries we are talking about--Guinea, Sierra Lione, and Liberia--is 22.136 million people, so the raw probability of a person from the heart of the epidemic having ebola is less than 0.0006. I suspect most people think that [$]t_u[$] is high--that they are likely to get ebola from someone who has it--and that [$]t_q[$] is zero--that putting someone in quarantine means they can't spread the disease. Neither is true. Out of thousands of contacts between the time of infection and the time of either death or recovery, the average ebola patient transmits the infection only twice--compared to 4 for HIV or 18 for measles, for some context--making for a relatively small transmission rate outside of quarantine. And the fact that some 521 out of roughly 3,000 health care workers--a much higher rate than the general public--got infected despite quarantines in place suggests that [$]t_q[$] is not that much lower than [$]t_u[$]. The reduction in the probability of transmission is [$]p\left(t_u-t_q\right),[$] and we've established that [$]t_q[$] is relatively high (certainly way higher than zero), so a quarantine can only be justified if [$]p[$] and [$]t_u[$] are large. That is, quarantines are only beneficial when a person is very likely to transmit an infection.
But of course, that is almost irrelevant given the added fact that asymptomatic individuals who have ebola are not infectious. Hence, [$]t_u=0[$] for the people we are talking about, and as a result, regardless of [$]I,[$] [$]p,[$] or [$]t_q,[$] it can't be net beneficial to quarantine these asymptomatic individuals.
So the case against quarantines of asymptomatic individuals returning from west Africa is
- The probability that they have ebola is small
- They aren't infectious even if they did have ebola
- Quarantines would not be that effective even if the subjects were infectious
- Quarantines are economically costly
- Quarantines discourage much-needed healthcare workers from volunteering to help figh ebola in africa
- Discouraging health workers imposes a high social cost because fighting ebola at the source in Sierra Lione, Liberia, and Guinea is by far the most effective way to stop the epidemic.
1 Not a typo.