arrow_back

Here's why advocating NGDP targeting is just plain silly

3/10/2014 02:22:00 PM
Tweetable
The Fed, attempting to follow through on a policy rule.
One of the raging debates in the macroeconomics profession right now--at least on the blogosphere--is whether the Federal Reserve and other central banks should adopt NGDP path targets, or some close variant thereof. While there are some variants, the general idea is that the Fed would choose a target growth rate for NGDP--the measure of total spending in the economy, unadjusted for inflation--of, say, 5 percent per year. The growth rate of NGDP is the sum of the inflation rate and the growth rate of real GDP, so 5 percent NGDP growth would correspond to 2 percent inflation and 3 percent economic growth, which are pretty average. Advocates like NGDP targeting because it would call for tightening when the economy is overheating--when either real GDP growth or inflation are higher than trend--and loosening monetary policy when the economy is weak--when inflation and/or real GDP growth are lower than trend. In that sense, NGDP targeting can be thought of as adopting an adjustable inflation rate target that depends on the rate of economic growth. I think Nick Rowe summed up why many economists are now thinking that NGDP targeting of some kind is the way to go--namely, it was the dog that barked when the economy was in trouble, while inflation remained silent.

I won't comment on how other central banks work, or whether other countries should adopt an NGDP target, but for the US I think this discussion is all pretty silly.

In the Macroeconomics research literature, it is customary to model the Fed as following what's called a "Taylor Rule," which is a rule that prescribes a particular interest rate target depending on certain objective, measurable inputs such as the unemployment rate and inflation. Many economists have estimated different versions of the Taylor Rule, but the best-estimated version I've seen, by far, is from Glen Rudebusch, a research economist at the Fed who estimated that this rule is the best fit for the Fed's choice behavior, out all possible Taylor-type rules:
r = π + 0.28 ( π − π * ) + 1.95 ( u * − u ) + 1.61
Now here's that in a graph:
You can compare Rudebusch's estimates to a few others here. But these estimates are much closer to actual Fed behavior than the others.
What you can see is that the FOMC actually deviates from the Taylor Rule quite a lot. And you can't just argue that the Fed is following a different Taylor Rule--Rudebusch estimated the one that minimizes the error term. The only way to interpret this is that the Fed doesn't actually follow any particular Taylor Rule at all. The economists are all just plain wrong. We can also tell that the Fed isn't following an inflation target or an NGDP target, because these series deviate quite a lot from trend too:
Nope, we don't already have an NGDP target. We don't even target inflation very well.
Maybe the Fed has some sophisticated optimal control policy rules designed to jointly minimize both inflation and output volatility? Well, Yellen derived that particular policy rule for us:
What was the point of highlighting an "optimal control path" if it isn't her actual recommendation?
...and then recommended against it:
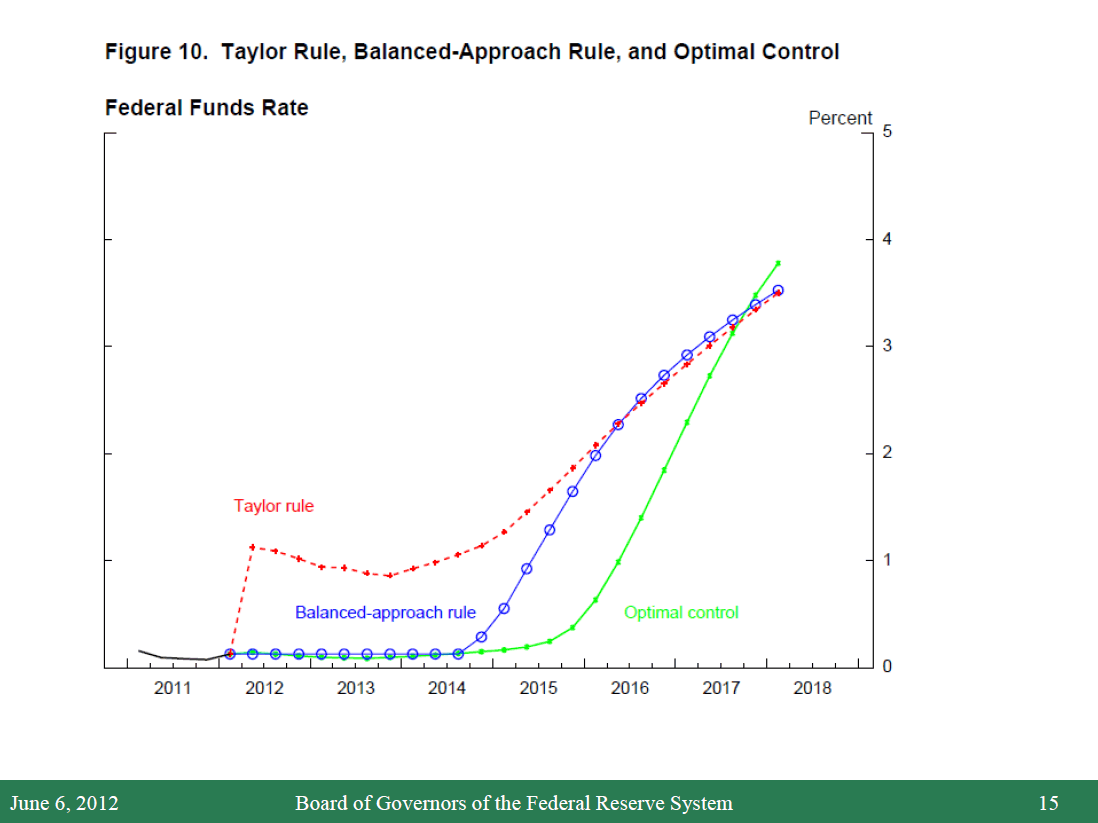
"Today, I will consider the prescriptions of two such benchmark rules--Taylor's 1993 rule, and a variant that is twice as responsive to economic slack. In my view, this latter rule is more consistent with the FOMC's commitment to follow a balanced approach to promoting our dual mandate, and so I will refer to it as the "balanced-approach" rule."
One explanation why the fed has failed to follow any consistent policy rule is because the Fed was incapable, for one reason or another, of doing so.

It could be that monetary policy simply isn't as potent as economists think, and the Fed's limited arsenal of policy instruments have little control over any of these time series. But I think Yellen's odd recommendation is very telling. She derived both an optimal control rule and a taylor rule, and then advocated a compromise path between the two. This tells me that Arrow's Theorem is dictating the Fed's behavior: Yellen could have chosen a loss function that would produce an optimal control path that corresponds to her actual policy recommendations--the choice of loss function was arbitrary and subjective. Instead she picked one that was more extreme than what she wanted as a way of changing the elements in the choice set before the FOMC. The preferences of the members of the FOMC are highly heterogeneous, meaning that, per Arrow's Theorem, by changing the set of possible choices Yellen also changed the median voter on the FOMC, and therefore changed the preferences of the FOMC as a whole.

To put it bluntly, Arrow's Theorem says that the FOMC is incapable of making rational, time-consistent choices, because it's preferences change depending on how the various choices are posed to the committee. This precludes any possibility of the FOMC committing to any monetary policy rule for long periods of time.

The preferences of the FOMC are quite heterogeneous. Of the current 10 voting FOMC members, only four were academic economists, and two others have previously held positions with the title "economist"--that means 4 members, nearly half the committee, are not economists (three lawyers and one banker). What economists think about monetary policy rules is less relevant to the FOMC than you might think, and there is quite a bit more disagreement within the FOMC than you might have suspected. This in itself is enough for Arrow's Theorem to bite, but we have to add in the fact that at the FOMC, the median voter literally gets changed out every year as membership rotates between different regional bank presidents on an annual basis. The Fed was designed in a way to guarantee it would be incapable of following a consistent policy rule.

So, in my view, debating which version of NGDP targeting would be optimal is a lot like the lazy fat guy looking for advice on how to improve his mile time. To have a mile time at all, he first needs to be able to run a mile! Similarly, for the Fed to adopt an NGDP target, it first needs to be able to commit to a policy rule. At present, that isn't possible.
Nick Rowe 3/11/2014 10:19:00 AM
So, other countries' central banks can target NGDP, inflation, a fixed exchange rate, a monetary aggregate, the price of gold, whatever, but the US central bank is congenitally incapable of following any sort of target, and can only act like an existentialist, for whom every day is a whole new day?

This sounds like an extreme form of American exceptionalism. OK, the US is different, and the Fed is set up differently from the Bank of Canada (it's a republic vs a monarchy), but the US is not some anarchic total mess of a country. You have the rule of law, and even a constitution. What are those things except a decision to keep Arrow under control?

The more people who see 5% NGDP as a Schelling focal point that frames the conversation, the closer it will be followed, even in anarchy. That's why society exists at all.
Matthew Martin 3/11/2014 11:56:00 AM
I didn't mean to imply that the US was exceptional in this regard--I merely limited my discussion to the US because I thought it would be presumptuous to say it is true of all central banks, and then only talk about the Federal Reserve. Moreover, Arrow's theorem may not apply to some central banks, such as china's, where Arrow's "dictator" isn't outside the realm of possibility.

Also, I don't doubt that, by altering the choice set, discussion of NGDP targeting can alter the Bank's behaviors--Arrow's Theorem says it will. My point is that we won't actually end up with an NGDP target because the committee's preferences will change as soon as any of the facts change.