How much larger should the stimulus have been?
In a follow up, Krugman gives us a back-of-the-envelope calculation for how big he thinks the ARRA spending provisions should have been. \$1.75 trillion spread over 18 quarters is the figure he gives.
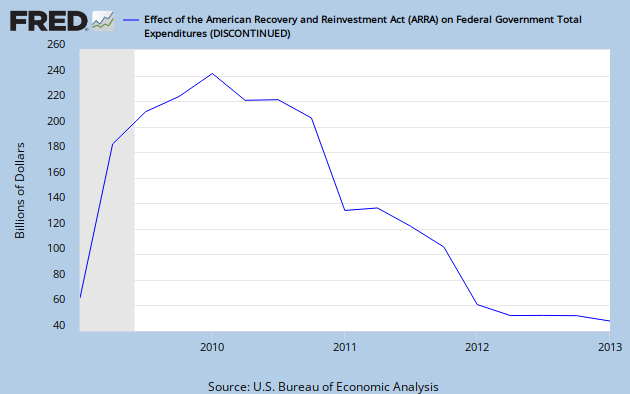
I mainly wrote this post to add a bit of perspective to Krugman's figure, since he never actually tells us how much spending the ARRA actually contained. Now, realize that the graph above is in annualized rates--meaning that the actual quarterly spending figures were a fourth of what the graph above shows. So I calculate a cumulative \$585.3 billion total spending in the ARRA, about a third of what Krugman claims was necessary.
There is an important caveat here, that Krugman failed to mention. These figures give an extremely myopic view of the ARRA's spending impacts. In particular, they only look at the impact on federal current expenditures, not total government consumption and investment expenditures, which is what really matters for Keynesian stimulus efforts. Case-in-point, about half that \$585.3 billion in "federal spending" was paid out in block grants to the states--to the extent states used these funds to offer tax cuts, they should be counted not as increased spending, but as decreased revenue. This is a warning against viewing economic discussions through myopic budget accounting rules.
Of course, Krugman also ignored the federal revenue side of the equation. FRED also claims to have this data here, which comes from the BEA report here, but disagrees with this other BEA report. The main discrepancy is that the payroll tax holiday was not part of the ARRA, but the two appear to disagree even excluding the payroll tax cut, and it's not totally clear to me why. Anyway, here's the impact of stimulus-related tax provisions, including tax provisions of ARRA as well as the payroll tax holiday, on current receipts:
These tax cuts involved marginal effective tax rate cuts for many millions of americans. The Making Work Pay Tax Credit reduced your taxes by 6.2 percent of income up to a total of \$400 in tax credits, meaning that this was an incentive to work more (effective marginal rate cut) for anyone earning less than \$6,450 per year in taxable income, which would include most students and temporary seasonal workers. The Payroll tax holiday of 2011 and 2012 reduced marginal effective tax rates by 2 percent of income for everyone earning less than \$110,100 per year, which is around 80 percent of the population.
Now, in normal times, these tax cuts would clearly be stimulative. They would encourage people to work more, and we'd see higher GDP as a result. But these were not normal times. And the evidence for expansionary marginal rate cuts in a liquidity trap is shaky at best. No empirical study has estimated the effect of marginal tax cuts during liquidity traps (they are much too rare for statistical analysis). However, the theory does not support the hypothesis: all of the modern liquidity trap models exhibit a property that Gauti Eggertson calls "paradox of toil" wherein a marginal tax rate cut actually decreases employment when we are at the zero lower bound. The reason for this is that tax cuts are deflationary, which means that at the zero lower bound when nominal interest rates cannot fall, a marginal tax rate cut actually increases the real interest rate, thereby reducing aggregate demand. It's not a result that all economists take seriously, but at present there's no clear evidence that it's wrong.
My point in bring up the paradox of toil is not to say that Casey Mulligan is wrong about everything, but that in fact, the predicted Keynesian effect is a wash. I already mentioned that half of the alleged \$585.3 billion "spending" in ARRA went actually went to states who used much of it to lower marginal tax rates. Add to this an additional \$269.4 billion in tax cuts from the Making Work Pay Tax Credit and Payroll tax holidays, and it is fairly ambiguous whether the stimulus efforts were mostly marginal tax rate reductions versus spending increases. And if, as New Keynesian theory suggests, marginal rate cuts are actually contractionary at the zero lower bound, then the net effect of the stimulus efforts on GDP is actually ambiguous: the contractionary effect of the tax cuts could easily be larger than the expansionary effects of the spending increases at the zero lower bound.
For this reason, I tend to think Christy Romer was right. Given these uncertainties, it would be far better to use the spending side of the ledger to engage in stimulus at the zero lower bound, and simply leave marginal tax rates at whatever we think they should be for the long-run. We should not attempt to use tax policy as a stimulus when we are at risk of hitting the zero lower bound.